Math 132: Smooth Manifolds, Spring 2017

Welcome to Math 132: Smooth Manifolds, Spring 2017! This course will be an introduction to some of the (geometric) methods of differential geometry and differential topology, following the excellent textbook Differential Topology by Guillemin and Pollack (AMS Chelsea Publishing, 2010 Edition).

Background Survey

Here's a snapshot of the responses regarding what aids your learning:

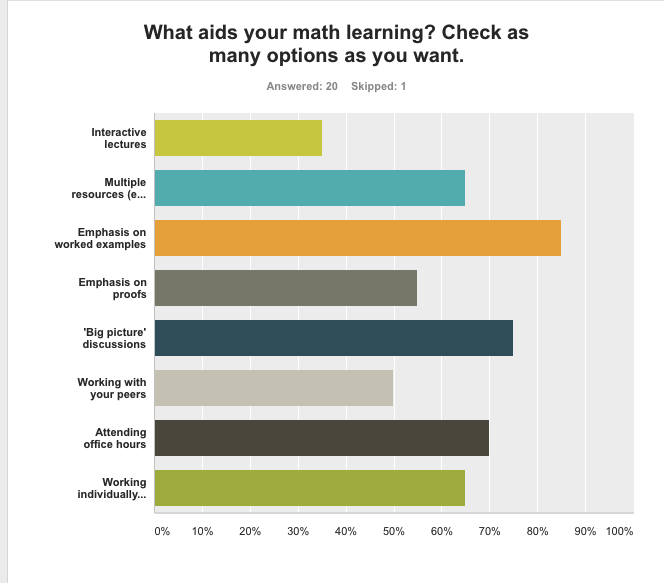
Here are your responses to the other feedback surveys

• Initial Feedback
• Homework Feedback

Course information:

• Syllabus
• Schedule
• Late Days Policy

A (Euclidean) manifold is a geometric object that locally looks like Euclidean n-space. Smooth manifolds are manifolds together with additional structure that allows us to do calculus. To a mathematician, the study of smooth manifolds is the branch of mathematics known as differential geometry and lies at the crossroads of geometry, analysis and partial differential equations (and beyond).

The methods of differential geometry abound in mathematics and the sciences: the resolution of the famous Poincaré conjecture followed from deep results in differential geometry; Einstein's theory of general relativity is formulated entirely in the language of differential geometry; differential geometry has been applied to understand the information content of DNA; differential topology (see below) arises in general equilibrium theory in microeconomics.

In this course, we will use the methods of differential geometry to understand the topology of a geometric object: we will relate infinitesimal information with global topological information. This is the realm of differential topology, an area of mathematics that has produced some of the most beautiful and astounding mathematics of the 20th century, and has latterly found deep connections with quantum field theory.

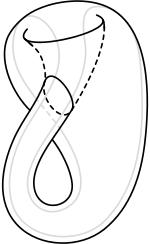
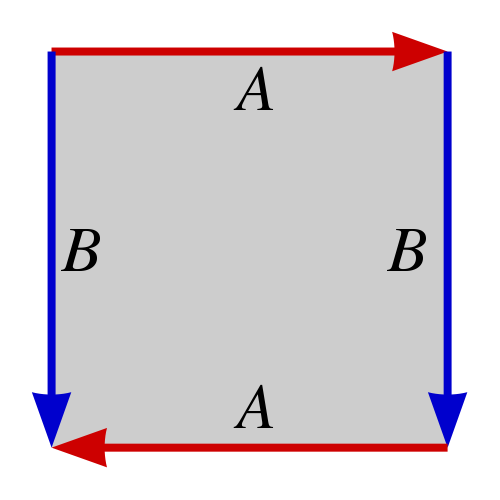
As a taster, consider the Klein bottle (pictured above): this is the compact surface constructed by gluing the boundary of the unit square, with identifications given below. Using oriented intersection theory students will prove that it is impossible to realise the Klein bottle as the zero locus in 3-d Euclidean space of a single function f(x,y,z).

Course Calendar