Proof of a Theorem on Looking at Prime Numbers

by Leonhard Euler

Commentaries of the Academy of Science of St. Petersburg, 8 (1736), 141-146

Translation by C. Edward Sandifer

Formerly most of the arithmetic theorems of Fermat were given without proofs, and perhaps they were true, and not just exceptional properties of certain numbers; Still, the science of numbers is itself valid, and seeing what the limits of Analysis of numbers ought to be vigorously sought. Although he gave remarkable discoveries of many things in geometry, theorems he asserted which he could prove, or at least which he was sure of their truth, for many it has been left to me to search for their proofs. Indeed, Fermat saw that most of his theorems would be proved by observation, for indeed that is nearly the only way the properties can be proved. In truth, it is possible to find examples in which observation may be used; from these one will suffice which Fermat himself is reported to have selected. I speak of course of that theorem whose falsity has only this year been announced, in which Fermat asserted that all numbers of the form tex2html_wrap_inline127 are prime numbers. In truth, observation is seen to suffice in proving this proposition.

For apart from the fact that all those prime numbers less than 100,000 are known, and it is easy to show that no prime number less than 600 can divide a number of the form tex2html_wrap_inline127 , however large a number is substituted for n. Nevertheless, it is easily seen that this proposition is not true, and the use of observation prevails in this kind of speculation.

For all these reasons, those properties of numbers which are shown only by observation for a long time have been judged to be uncertain, until either a direct proof has been build or they are altogether disproved. Yet there are no theorems which I have found in those pages of the memorable theorems of Fermat but those which are connected with, to be faithful to the judgment, observation. and which knowledge of their truth is discovered by observation. In fact since I am most firmly adept at these particular proofs of these theorems, their truth is not at all doubtful. Wherefore, thus, the truth of that theorem is made plain by that method, the proofs of which I have set forth, and it can contribute strongly in other investigations of numbers, as I will show in this dissertation.

The proposition which I have supported with this proof is the following:

If p is a prime number in the formula tex2html_wrap_inline135 , then this number is always divisible by p, unless a can be divided by p.

In this way alone, the truth of the remainder of the proof of this theorem flows. In the case of the formula where a=2, the proof of the theorem will be given, and this proof cannot extend to the general formula. For which reason the proof will be given in the case of this prime, to make easier the transition to the general case. Therefore the following proposition will be proved:

If p is an odd prime number, then the formula tex2html_wrap_inline147 can always be divided by p.

PROOF

In place of 2 write 1+1 and get

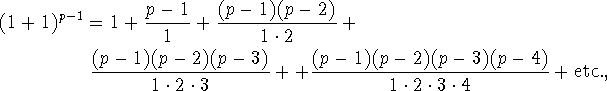
multline25

The number of terms in this series is p, and is thus odd. Moreover, any term which has the form of a fraction gives an integer number since the numerator is always divisible by its denominator. Cutting off the first term, 1, of this series gives

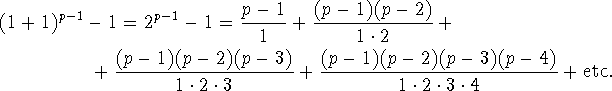
multline36

The number of terms of this series is p-1, and is thus even. Thus, collecting pairs of terms into one sum, so the number of terms will be half as many, gives

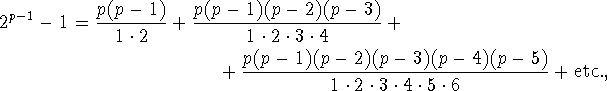
multline48

Since p is an odd number, the last term of this series will be

displaymath121

It now becomes visible that each term is divisible by p, since p is a prime number larger than any factor in the denominator, so division by the denominator cannot eliminate the factor. For that reason, if p is an odd prime number, then tex2html_wrap_inline147 may always be divided by it. Q. E. D.

In another way, if tex2html_wrap_inline147 can be divided by a prime number p, so also, in turn, will be its double, tex2html_wrap_inline175, and so (see note)

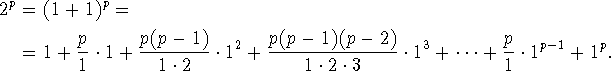
multline64

Cutting off the first and last terms of this series gives

displaymath122

Looking at this series, each term is divisible by p, since p is a prime number. Thus always tex2html_wrap_inline175 can be divided by p, unless p=2. Q. E. D.

Since tex2html_wrap_inline147 can be divided by an odd prime, it is easily known that p divides any formula tex2html_wrap_inline191 , where m denotes any integer whatsoever. Thus the prime number p can divide the following forms tex2html_wrap_inline195 , tex2html_wrap_inline197 , tex2html_wrap_inline199 etc. Therefore the truth of this theorem is proved in general for all cases where a is any power of 2 and p is a prime number except two.

We will now prove the following

THEOREM

Denoting by p any prime number except 3, the formula tex2html_wrap_inline211 can always be divided by p.

PROOF

If tex2html_wrap_inline211 is divisible by a prime number other than 3, then tex2html_wrap_inline219 is divisible by it, and conversely. It is true then that

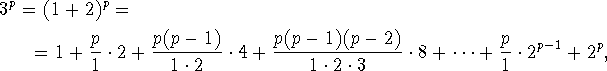
multline92

in which series each term except the first and the last is divisible by p, if p is a prime number. Therefore the formula tex2html_wrap_inline225 is divisible by p, which is equal to this:

displaymath123

And tex2html_wrap_inline175 is always divisible by the prime number p, and so also is tex2html_wrap_inline219.

And so tex2html_wrap_inline211 is always divisible by p, as long as p is a prime number other than 3. Q. E. D.

In this manner it is possible to progress from a given value a to the value one greater. But by this proof one may produce a general theorem by putting together carefully larger and larger numbers, which leads to the following

THEOREM

Denoting by p a prime number, if tex2html_wrap_inline245 can be divided by p, then so also can the formula tex2html_wrap_inline249.

PROOF

tex2html_wrap_inline251 is resolved into a series in the usual way to get

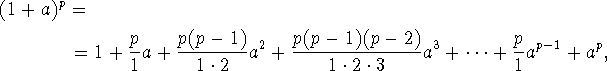
multline106

in which series each term is divisible by p except the first and the last, if p is a prime number. For that reason, tex2html_wrap_inline257 can be divided by p, and this formula is the same as tex2html_wrap_inline261 . And tex2html_wrap_inline245 can be divided by p, by hypothesis, and therefore tex2html_wrap_inline267 can be also. Q. E. D.

Therefore, with the knowledge that ap-a can be divided by the prime number p, it admits the division of tex2html_wrap_inline249 by p, and it follows tex2html_wrap_inline275 , and then tex2html_wrap_inline277 and generally tex2html_wrap_inline279 to be divisible by p. Putting a=2, and we have already shown that tex2html_wrap_inline175 can be divided by p, and it follows that the formula tex2html_wrap_inline289 ought to admit division by p, whatever number is substituted in place of b.

Therefore p divides tex2html_wrap_inline245 , and consequently tex2html_wrap_inline135 , unless a=p or a is a multiple of p.

And so this is a proof of the general theorem, which I have handed down for posterity.

Translated by C Edward Sandifer

August 20, 1996

Note:
Sandifer's text is missing the next two displayed formulas, which I have supplied from the sense of the argument, without checking with the original-FQG.

Fernando Q. Gouvêa ---- fqgouvea@colby.edu
Last modified: Fri Dec 5 10:12:26 1997