MA177--What Fermat says
Here is a compilation of the assertions made by Fermat about
numbers. Almost all of them come from the texts you read last week, but I
couldn't resist adding a couple.
Some natural questions to ask about each of these assertions are:
- Where did Fermat find this?
- Is it true?
- Can I prove it's true? (or false?)
- Why is this an interesting question?
As you can see from Pascal's letter, not everyone thought these were
interesting questions!
- The number
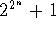 is always a prime
number.
is always a prime
number.
- Every number is the sum of at most three triangular numbers.
Note: if we declare that 0 is a triangular (square, pentagonal,
...) then we can drop the ``at most'' from all these assertions.
People in Fermat's time were still a little suspicious of 0 as a
number.
- Every number is the sum of at most four squares.
- Every number is the sum of at most five pentagonal numbers.
- Etc.
- A prime number of the form p=4k+1 (one more than a
multiple of four) can be obtained as the sum of two squares, i.e.,
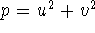 , where u and v are whole numbers.
, where u and v are whole numbers.
- A prime number of the form p=3k+1 can be expressed as
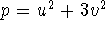 , where u and v are whole numbers.
, where u and v are whole numbers.
- A prime number which is either of the form p=8k+1 or
p=8k+3 can be expressed as
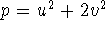 ,
where u and v are whole numbers.
,
where u and v are whole numbers.
- A right triangle whose sides have whole number lengths cannot have
area equal to a square. (For example, if the triangle has sides
equal to 3, 4, and 5 units then its area is 6, which isn't a square.
- Fix a prime number p, and consider the sequence of powers of 2:
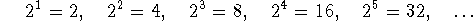
Then:
- There is always a smallest exponent n such that
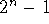 is a multiple of p.
is a multiple of p.
- This n is always a divisor of p-1.
- If m is any other exponent such that
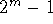 is a multiple of p, then m is
a multiple of n.
is a multiple of p, then m is
a multiple of n.
- The statements above remain true when we replace 2 with any other
number that is not divisible by our prime number p.
- Given any number N that is not a square, there exist infinitely
many pairs of whole numbers x and y such that
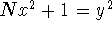 .
.
- In the previous problem, there exists an explicit ``mechanical''
procedure for finding all the solutions x and y.
- No cube can be written as a sum of two cubes.
- No fourth power can be written as a sum of two fourth powers.
- In general, if n is bigger than 2, no n-th power can
be written as the sum of two n-th powers.
Fernando Q. Gouvea
Fri Nov 21 13:32:48 EST 1997
![]()
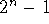 is a multiple of p.
is a multiple of p.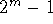 is a multiple of p, then m is
a multiple of n.
is a multiple of p, then m is
a multiple of n.