MA177---What to look for in Newton and Berkeley

Monday we'll discuss Newton's ``Lemma II'' and Berkeley's ``The Analyst.'' Here are a few things to look for as you read (or re-read) these texts.

1. What Newton calls a ``genitum'' is just a product of powers 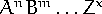where there can be lots of factors and the exponents are of any kind. The point of the Lemma is to determine the fluxion (or the differential) of such a quantity.

2. What Newton calls a ``moment'' is essentially a Leibniz-style differential: it's the amount an object ``wants to change'' when it just begins to change. In the ``o'' notation, it's , in the sense that as time moves from t to t+o, the fluent x ``wants to'' become (of course, this isn't exactly right, but it gets closer to being right as the increment o gets closer to zero...).

3. The most important part of the proof is ``Case 1'' on page 2. Make sure you understand. Compare with Leibniz's rule for the differential of a product.

4. In Cases 2-6, Newton basically uses Case 1 over and over again to establish more complicated cases.

5. Don't worry about the Corollaries on page 3.

6. In ``The Analyst,'' Berkeley starts by giving his purpose in writing; what is it?

7. Berkeley then tries to figure out what is meant by ``moment,'' ``fluxion,'' and so on. What does he conclude?

8. Notice that pages 7/8 were bound in backwards, so page 8 comes before page 7!

9. In sections 9-12, Berkeley discusses Newton's argument in Case 1 of ``Lemma II'' and its consequences. What does he make of Newton's argument?

10. In sections 13-16, Berkeley goes over the bit we did in class to compute the fluxion of 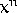. What is his argument?

11. Section 20 is important. What is Berkeley's main position?

12. How does Berkeley explain the fact that the calculus works?